CEopt

Logo

CEopt is a Matlab routine for nonconvex optimization using the Cross-Entropy method and augmented Lagrangian formulation.

View the Project on GitHub americocunhajr/CEopt

Cross-Entropy Optimizer

CEopt: Cross-Entropy Optimizer is a Matlab package that implements a framework for nonconvex optimization using the Cross-Entropy (CE) method. Due to the algorithm’s relative simplicity, CEopt provides a transparent “gray-box” optimization solver with intuitive control parameters. It effectively handles both equality and inequality constraints through an augmented Lagrangian method, offering robustness and scalability for moderately sized complex problems. CEopt’s applicability and effectiveness are demonstrated through select case studies, making it a practical addition to optimization research and application toolsets.

Table of Contents

Overview

CEopt was developed to provide a robust and scalable solution for nonconvex optimization problems using the Cross-Entropy method. More details can be found in the following paper:

Preprint available at: https://doi.org/10.48550/arXiv.2409.00013

Features

Installation

To install and get started with CEopt, follow these steps:

  1. Clone the repository: 
    git clone https://github.com/americocunhajr/CEopt.git
  2. Navigate to the package directory: 
    cd CEopt/CEopt-1.0
  3. Copy the CEopt.m file to your working directory: 
    cp CEopt.m 'path_to_working_directory'

Alternatively, you can add the CEopt directory to the Matlab path:

  1. Open Matlab and type 
    addpath 'path_to_CEopt_directory/CEopt/CEopt-1.0'

    This will add CEopt to the path for the running section. Every time MATLAB is restarted this procedure must be repeated.

Usage

To run CEopt, use the following commands in Matlab:

   [Xopt,Fopt,ExitFlag,CEstr] = CEopt(fun,xmean0,sigma0,lb,ub,nonlcon,CEstr)

Each parameter is described as follows:

The CEstr structure allows for extensive customization of the CE optimization process. Here’s a breakdown of its fields:

This extensive set of parameters and settings enables users to finely tune the CE optimization to their specific needs and problem characteristics.

Examples

Below are step-by-step guides demonstrating how to use CEopt for different optimization tasks.

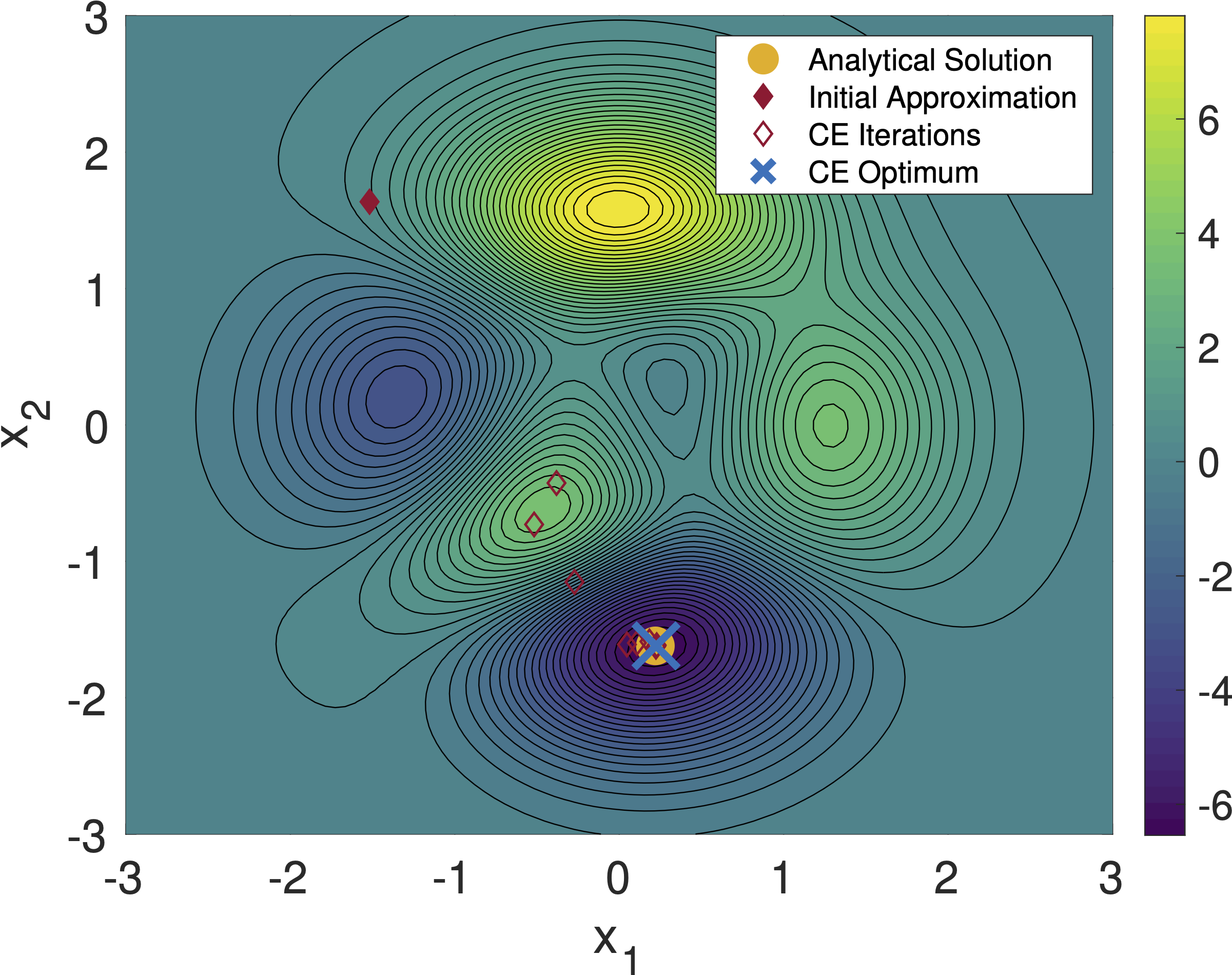
% Unconstrained optimization with 2 variables

% objective function
F = @(x)PeaksFunc(x);

% bound for design variables
lb = [-3; -3];
ub = [ 3;  3];

% initialize mean and std. dev. vectors
mu0    = lb + (ub-lb).*rand(2,1);
sigma0 = 5*(ub-lb);
        
% define parameters for the CE optimizer
CEstr.isVectorized = 1;       % Vectorized function
CEstr.EliteFactor  = 0.1;     % Elite samples percentage
CEstr.Nsamp        = 50;      % Number of samples
CEstr.MaxIter      = 80;      % Maximum of iterations
CEstr.TolAbs       = 1.0e-2;  % Absolute tolerance
CEstr.TolRel       = 1.0e-2;  % Relative tolerance
CEstr.alpha        = 0.7;     % Smoothing parameter
CEstr.beta         = 0.8;     % Smoothing parameter
CEstr.q            = 10;      % Smoothing parameter

% CE optimizer
tic
[Xopt,Fopt,ExitFlag,CEstr] = CEopt(F,mu0,sigma0,lb,ub,[],CEstr)
toc

% objective function
function F = PeaksFunc(x)
    x1 = x(:,1);
    x2 = x(:,2);
     F = 3*(1-x1).^2.*exp(-x1.^2 - (x2+1).^2) ...
       - 10*(x1/5 - x1.^3 - x2.^5).*exp(-x1.^2 - x2.^2)...
       - (1/3)*exp(-(x1+1).^2 - x2.^2);
end


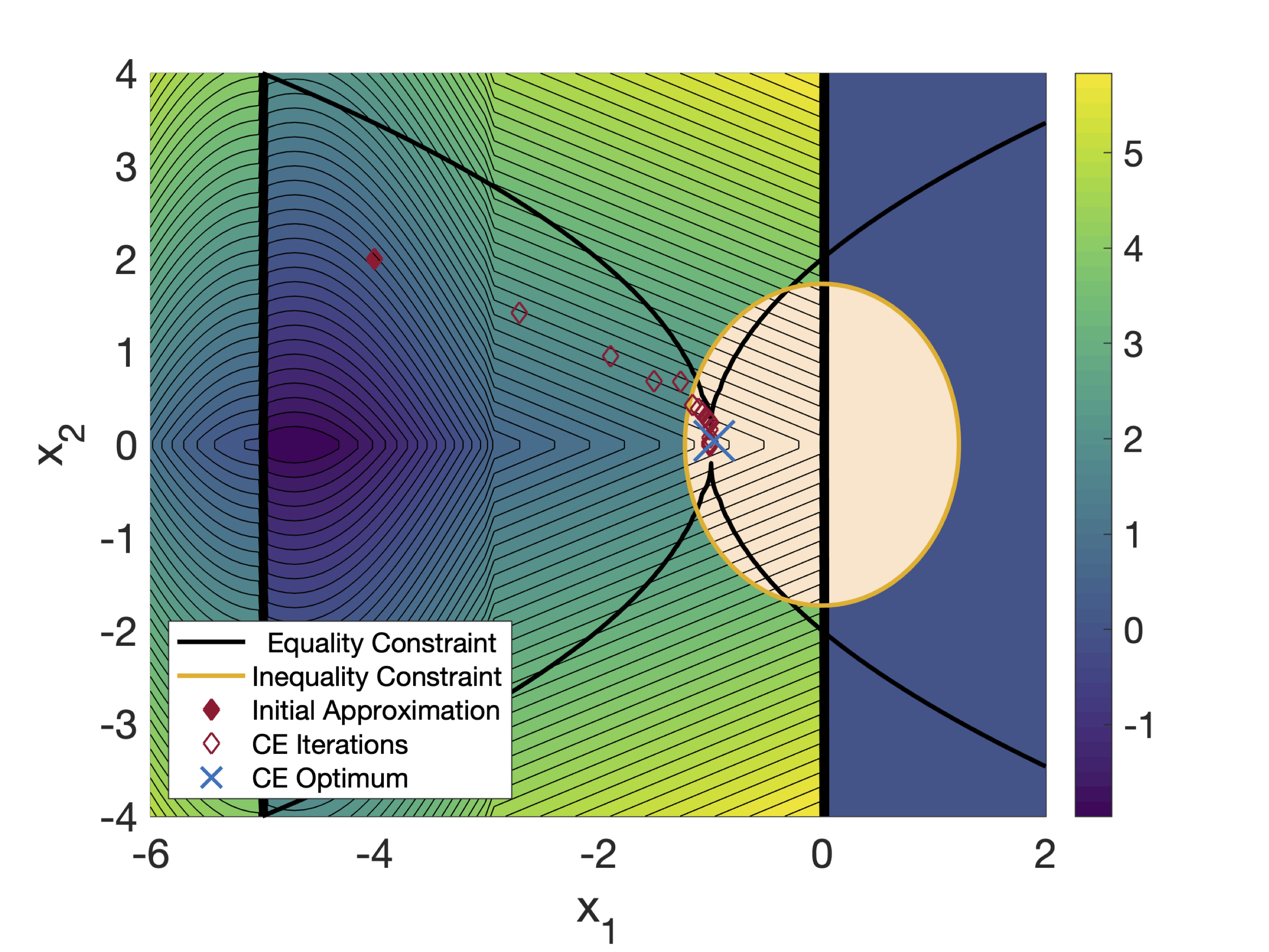
% Constrained optimization with 2 variables

% objective function and constraints
F       = @PatternSearchFunc;
nonlcon = @ConicConstraints;

% bound for design variables
lb  = [-6 -4];
ub  = [ 2  4];
mu0 = [-4  2];

% cross-entropy optimizer struct
CEstr.isVectorized  = 1;       % vectorized function
CEstr.TolCon        = 1.0e-6;  % relative tolerance

tic
[Xopt,Fopt,ExitFlag,CEstr] = CEopt(F,mu0,[],lb,ub,nonlcon,CEstr)
toc

% objective function
function F = PatternSearchFunc(x)
    x1 = x(:,1);
    x2 = x(:,2);
    F = zeros(size(x1,1),1);
    for i = 1:size(x,1)
        if  x1(i) < -5
            F(i) = (x1(i)+5).^2 + abs(x2(i));
        elseif x1(i) < -3
            F(i) = -2*sin(x1(i)) + abs(x2(i));
        elseif x1(i) < 0
            F(i) = 0.5*x1(i) + 2 + abs(x2(i));
        elseif x1 >= 0
            F(i) = .3*sqrt(x1(i)) + 5/2 + abs(x2(i));
        end
    end
end

% equality and inequality constraints
function [G,H] = ConicConstraints(x)
    x1 = x(:,1);
    x2 = x(:,2);
    G  = 2*x1.^2 + x2.^2 - 3;
    H  = (x1+1).^2 - (x2/2).^4;
end

Note on Stochastic Nature of CEopt

The CE method, which underpins the CEopt package, is inherently stochastic. This means that each run of the optimization process might follow a different trajectory towards the optimum due to the random sampling involved in the method. Therefore, it is entirely normal for repeated executions of the same optimization task to yield different paths or convergence profiles. Users are encouraged to consider multiple runs or adjust the sigma0 parameter to manage the exploration-exploitation balance and potentially achieve more consistent results.

Reproducibility

The tutorials of CEopt package are fully reproducible. You can find a fully reproducible capsule of the simulations on CodeOcean.

Documentation

The routines in CEopt package are well-commented to explain their functionality. Each routine includes a description of its purpose, as well as inputs and outputs. Detailed documentation about the code functionality can be found in paper.

Authors

Citing CEopt

If you use CEopt in your research, please cite the following publication:

@article{CunhaJr2024CEopt,
   author  = {A {Cunha~Jr} and M. V. Issa and J. C. Basilio and J. G. {Telles Ribeiro}},
   title   = "{CEopt: A MATLAB Package for Non-convex Optimization with the Cross-Entropy Method}",
   journal = {PrePrint},
   year    = {2024},
   volume  = {arXiv:2409.00013},
   pages   = {~},
   doi    = {10.48550/arXiv.2409.00013},
}

License

CEopt is released under the GNU General Public License v3.0. See the LICENSE file for details. All new contributions must be made under the MIT license.

Institutional support

Funding

         

Contact

For any questions or further information, please contact:

Americo Cunha Jr: americo.cunha@uerj.br